初めまして、しょうがといいます。
興味のあるもの:
・数理モデリング
・細胞
・システム
・物理生物学
・サピアウォーフ仮設
・人工言語(ロジバン
ただいま大学4回生。実験室の日々
2020年1月1日水曜日
2014年8月12日火曜日
numpyとscipyのヒストグラム
numpy.histogram()の仕様を自分用に和訳。
http://docs.scipy.org/doc/numpy/reference/generated/numpy.histogram.html
---
numpy.histogram(a, bins=10, range=None, normed=False, weights=None, density=None)
#パラメータについて
a : array様シーケンス(おそらく普通のリストでもいいってことだと思う)
入力データ。aが二次元以上の場合、平坦化してから計算される。
bins : int もしくは尺のシーケンス(省略可)
intの場合、そのintは階級数(bins)の個数を規定する。(デフォルトで10階級)
シーケンスの場合、そのシーケンスの値は階級境界(bins edges)を規定する。ただし、最右端もそのシーケンスに含まれなければならない。非均等幅も可能。
range : (float, float) (省略可)
binsの最小と最大値。デフォルトでは、単純に(a.min(), a.max())が与えられる。
normed:
バグとか混乱が大きいため、numpy 2.0以降では廃止[なので訳さない。]
weights : array様シーケンス
重みの配列で、aと同じ形をしているシーケンスをとる。aのそれぞれの値は度数のカウントの際にその重み倍されて数えられる。
density : bool(省略可)
Trueにすると、度数の代わりにその階級での規定した幅の全面積が1になるような確率密度関数の値が出力される。単位幅(unity width)の階級が選ばれていない限り、度数の総和が1にならないことに注意。すなわち、確率質量関数ではない。[つまり、density=Trueにした場合は、得られた値×階級幅が相対度数になるのかな?まあ相対度数グラフならdensity=Falseで度数リストもらってから、それをデータ数で割ったほうが簡単そうだ。]
#返り値
hist : array
度数。
bin_edges : array of dtype float
階級境界の値(最右端も含む)
-------------------------------------
scipy.stats.histogram()も存在した!
何が違うのかよくわからんので、とりあえず和訳。
http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.histogram.html
---
scipy.stats.histogram(a, numbins=10, defaultlimits=None, weights=None, printextras=False)
指定された範囲をいくつかの階級にわけ、それぞれの階級の度数を返す。
#パラメータ:
a : array様シーケンス
データの配列
numbins : int (省略可)
階級の数。デフォルトは10
defaultlimits : タプル (lower, upper) (省略可)
ヒストグラムの範囲の最小値と最大値。省略した場合は、データの範囲(max(a)-min(a))よりわずかに広めに範囲が設定される。
特に、(a.min() - s, a.max() + s),
ここで s = (1/2)(a.max() - a.min()) / (numbins - 1).
weights : array様シーケンス(省略可)
aのそれぞれの値に対する重み。デフォルトだと無し、すなわち、それぞれに1倍の比重をかける。
printextras : bool(省略可)
Trueにした場合、除外点(extra points)(設定した範囲から漏れたデータ)があるときにその数をprintする。デフォルトはFalse.
#返り値:
histogram : ndarray
それぞれの階級の度数(もしくは重み付き度数)
low_range : float
ヒストグラムの階級境界の最小値(最左端)。
binsize : float
階級幅(the size of the bins)。すべての階級は等幅である。
extrapoints : int
ヒストグラムの範囲から漏れたデータの個数
--------------------------------------
#どっちを使うべきなんだろう
とりあえず、numpyのほうは非均等階級幅が設定できるのが強み(?)でも使うことあんのか。
その自由性があるから階級境界値もシーケンスでリターンするんだね。
しかし、numpyのほうは最右端の値も度数としてカウントするという、データの階級への入れ方が非均等なのであまりすきじゃない。しかも、ヒストグラム書くときのルールである「階級境界はデータの0.5単位下にとる」というのをガン無視してるので。
そう考えると、scipyのほうがより正確。ヒストグラムの範囲をデータ範囲より若干広く取るので。さらに非均等幅の設定はできないので、返り値もシンプル。ただ、グラフ書くときはちょっとめんどくさそう。
>>> data = np.random.randint(0,10,20)
>>> data
array([0, 2, 4, 9, 1, 0, 0, 6, 7, 8, 5, 3, 9, 7, 6, 3, 4, 9, 8, 0])
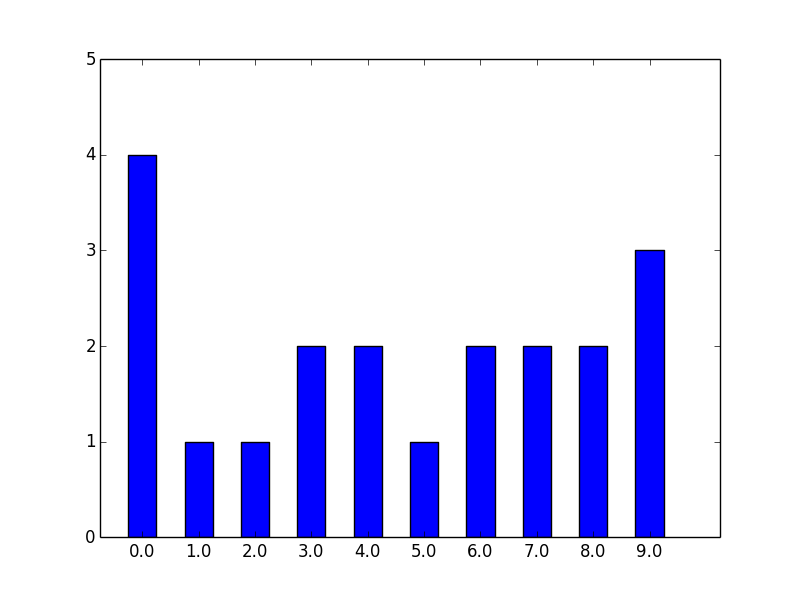
>>> stats.histogram(data)
(array([ 4., 1., 1., 2., 2., 1., 2., 2., 2., 3.]), -0.5, 1.0, 0)
>>> his_f, his_amin, his_d = stats.histogram(data)[:-1]
諸々の値デフォルト(階級数10)で度数分布作ったの図。
階級境界最小値は-0.5, 階級幅は1.0から、ヒストグラムの横軸を作れるはず。
とりあえず、numpyの返り値である、bin_edgeの最右端の無いバージョンは、
>>> bin_edge = np.array([his_amin + his_d * i for i in range(np.size(his_f))])
array([-0.5, 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5])
とすれば求まるし、階級値c(階級境界の中点)は、
>>> his_c = bin_edge + np.ones(np.size(his_f))*0.5*his_d
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
とすればよい。ここまでくれば、あとはnumpyと同様、
>>> pl.bar(his_c,his_f)
でおk。pl.xlim, pl.ylim, pl.xticks, pl.yticks などはお好みでどうぞ。
一例を下に。
としてやれば、
numbinsはデフォルトで10ではあるが、実際は平方根則やらスタージェスの公式を使ったほうがいいかもしんないね!
http://docs.scipy.org/doc/numpy/reference/generated/numpy.histogram.html
---
numpy.histogram(a, bins=10, range=None, normed=False, weights=None, density=None)
#パラメータについて
a : array様シーケンス(おそらく普通のリストでもいいってことだと思う)
入力データ。aが二次元以上の場合、平坦化してから計算される。
bins : int もしくは尺のシーケンス(省略可)
intの場合、そのintは階級数(bins)の個数を規定する。(デフォルトで10階級)
シーケンスの場合、そのシーケンスの値は階級境界(bins edges)を規定する。ただし、最右端もそのシーケンスに含まれなければならない。非均等幅も可能。
range : (float, float) (省略可)
binsの最小と最大値。デフォルトでは、単純に(a.min(), a.max())が与えられる。
normed:
バグとか混乱が大きいため、numpy 2.0以降では廃止[なので訳さない。]
weights : array様シーケンス
重みの配列で、aと同じ形をしているシーケンスをとる。aのそれぞれの値は度数のカウントの際にその重み倍されて数えられる。
density : bool(省略可)
Trueにすると、度数の代わりにその階級での規定した幅の全面積が1になるような確率密度関数の値が出力される。単位幅(unity width)の階級が選ばれていない限り、度数の総和が1にならないことに注意。すなわち、確率質量関数ではない。[つまり、density=Trueにした場合は、得られた値×階級幅が相対度数になるのかな?まあ相対度数グラフならdensity=Falseで度数リストもらってから、それをデータ数で割ったほうが簡単そうだ。]
#返り値
hist : array
度数。
bin_edges : array of dtype float
階級境界の値(最右端も含む)
-------------------------------------
scipy.stats.histogram()も存在した!
何が違うのかよくわからんので、とりあえず和訳。
http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.histogram.html
---
scipy.stats.histogram(a, numbins=10, defaultlimits=None, weights=None, printextras=False)
指定された範囲をいくつかの階級にわけ、それぞれの階級の度数を返す。
#パラメータ:
a : array様シーケンス
データの配列
numbins : int (省略可)
階級の数。デフォルトは10
defaultlimits : タプル (lower, upper) (省略可)
ヒストグラムの範囲の最小値と最大値。省略した場合は、データの範囲(max(a)-min(a))よりわずかに広めに範囲が設定される。
特に、(a.min() - s, a.max() + s),
ここで s = (1/2)(a.max() - a.min()) / (numbins - 1).
weights : array様シーケンス(省略可)
aのそれぞれの値に対する重み。デフォルトだと無し、すなわち、それぞれに1倍の比重をかける。
printextras : bool(省略可)
Trueにした場合、除外点(extra points)(設定した範囲から漏れたデータ)があるときにその数をprintする。デフォルトはFalse.
#返り値:
histogram : ndarray
それぞれの階級の度数(もしくは重み付き度数)
low_range : float
ヒストグラムの階級境界の最小値(最左端)。
binsize : float
階級幅(the size of the bins)。すべての階級は等幅である。
extrapoints : int
ヒストグラムの範囲から漏れたデータの個数
--------------------------------------
#どっちを使うべきなんだろう
とりあえず、numpyのほうは非均等階級幅が設定できるのが強み(?)でも使うことあんのか。
その自由性があるから階級境界値もシーケンスでリターンするんだね。
しかし、numpyのほうは最右端の値も度数としてカウントするという、データの階級への入れ方が非均等なのであまりすきじゃない。しかも、ヒストグラム書くときのルールである「階級境界はデータの0.5単位下にとる」というのをガン無視してるので。
そう考えると、scipyのほうがより正確。ヒストグラムの範囲をデータ範囲より若干広く取るので。さらに非均等幅の設定はできないので、返り値もシンプル。ただ、グラフ書くときはちょっとめんどくさそう。
>>> data = np.random.randint(0,10,20)
>>> data
array([0, 2, 4, 9, 1, 0, 0, 6, 7, 8, 5, 3, 9, 7, 6, 3, 4, 9, 8, 0])
>>> stats.histogram(data)
(array([ 4., 1., 1., 2., 2., 1., 2., 2., 2., 3.]), -0.5, 1.0, 0)
>>> his_f, his_amin, his_d = stats.histogram(data)[:-1]
諸々の値デフォルト(階級数10)で度数分布作ったの図。
階級境界最小値は-0.5, 階級幅は1.0から、ヒストグラムの横軸を作れるはず。
とりあえず、numpyの返り値である、bin_edgeの最右端の無いバージョンは、
>>> bin_edge = np.array([his_amin + his_d * i for i in range(np.size(his_f))])
array([-0.5, 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5])
とすれば求まるし、階級値c(階級境界の中点)は、
>>> his_c = bin_edge + np.ones(np.size(his_f))*0.5*his_d
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
とすればよい。ここまでくれば、あとはnumpyと同様、
>>> pl.bar(his_c,his_f)
でおk。pl.xlim, pl.ylim, pl.xticks, pl.yticks などはお好みでどうぞ。
一例を下に。
import numpy as np
from scipy import stats as stats
import pylab as pl
data = np.array([0, 2, 4, 9, 1, 0, 0, 6, 7, 8, 5, 3, 9, 7, 6, 3, 4, 9, 8, 0])
bins = 10
his_f, his_amin, his_d =stats.histogram(data, numbins=bins)[:-1]
bin_edge = np.array([his_amin+his_d*i for i in range(bins)])
his_c = bin_edge + np.ones(bins)*0.5*his_d
bar_width = 0.5
pl.xlim(min(bin_edge)-0.5,max(bin_edge) + his_d + 0.5)
pl.ylim(0,max(his_f)+1)
pl.xticks(bin_edge + np.ones(bins)*bar_width*0.5, his_c)
pl.bar(bin_edge, his_f, width = bar_width)
xtickでx軸の目盛りは色々変えれるはず。
階級範囲を示しておきたい(普通はこれがベターかも)なら、
xticks_label = [str(i)+"~"+str(i+his_d) for i in bin_edge]
pl.xticks(bin_edge + np.ones(bins)*bar_width*0.5, xticks_label)
としてやれば、
みたいな感じでいけます。内包表記って便利だなあ!
2014年6月6日金曜日
グレた確率統計 ~ポアソン分布~
これまでにしてきたことを少し振り返ってみましょう。
まず、ベルヌーイ試行から始まりました。ONかOFFか、YESかNOか、1か0か、というやつですね。それを複数回行ったときのONの数の確率分布を求めました(二項分布)。そして、初めてONが出たときの試行回数の確率分布も求めました(幾何分布)。畳み込みを踏まえた上で、幾何分布の一般形、すなわち r回ONが出たときの試行回数の確率分布も求めました(負の二項分布)。そのあと、連続化に進み、幾何分布を連続化しました(指数分布)。また、負の二項分布の連続化、もしくは指数分布の畳み込みを行いました(アーラン分布)。
二項分布、幾何分布、負の二項分布、指数分布、アーラン分布が、単純なベルヌーイ試行から導出されてきたことを見てきたわけです。
さて、今回は、次のような分布を求めてみます。すなわち、「単位時間で事象がk回起こる確率」です。
最も単純明快な導出方法は、おそらく、アーラン分布(ガンマ分布)を用いたものでしょう。
単位時間で事象がk回起こる確率というのは、t' < 1 なる t' でk回起こり、残りの時間は起こらなかった確率と言い換えられます。t = t' で k回起こる確率というのはガンマ分布、
$$\Gamma(t; r=k) = \frac{t^{k-1} \phi^{k} \exp(-\phi t)}{(k-1)!}$$
で表わせ、残りの時間、すなわち t = 1-t' で1回も起こらない確率$g_0(t)$は指数分布を用いて、
$$g_0(t) = 1-\int_0^t \phi \exp(-\phi t') dt' = \exp(-\phi t)$$
とできますから、この2つの畳込み、
$$Pr(X=k) = \int_0^1 \Gamma(t';r=k)\cdot g_0 (1-t')dt' \\ = \int_0^1 \frac{t'^{k-1} \phi^{k} \exp(-\phi t')}{(k-1)!} \cdot \exp(-\phi (1-t')) dt' \\ = \frac{\phi^k \exp(-\phi)}{(k-1)!} \int_0^1 t'^{k-1}dt' = \frac{\phi^k}{k!} \exp(-\phi) $$
この分布をポアソン分布といい、意味としてはさきに書いた通り、「単位時間で事象がk回起こる確率」となります。
というわけで、主要な確率分布が以上のようにすべて繋がっているように考えられるということが分かります。
(多分おしまい)
グレた確率統計 ~ガンマ・アーラン分布~
前回は、幾何分布から指数分布へ、つまり離散型から連続型への変換をやりました。
幾何分布は畳み込むことで負の二項分布になりましたね。
もちろんのことながら、負の二項分布を連続化した分布も考えることができます。
さらに言えば、指数分布を畳み込むことで同じ分布が得られるはずです。
それこそがガンマ分布(厳密に言えばアーラン分布)なわけです。
そこで、ここではガンマ分布を2つのやり方
① 負の二項分布の連続化
② 指数分布の畳み込み
で導出してみます。
$$Pr(X=k) = ~{}_{k-1} \mathrm{C}_{r-1} ~ p^r q^{k-r}$$
と表わせ、「事象が試行k回目にちょうどr回生じる確率」の意味付けができます。
これを連続化すれば、おそらく
「事象が時間tのときにちょうどr回生じる確率分布」が得られるはずです。
まず、組み合わせの変形はそのままではやりづらいので、負の二項分布の自然対数を変形していくことにします。
また、非常に大きい数 x について、スターリンの近似式、
$$ \ln x! \approx x \ln x - x$$
が成り立つこと、そして、小さい数 x について、次の近似式が成り立ちます:
$$ \ln (1-x) \approx -x $$
$$\ln Pr(X=k) = \ln \left( ~{}_{k-1} \mathrm{C}_{r-1} ~ p^r q^{k-r} \right) = \ln \left( \frac{(k-1)!}{(k-r)! (r-1)!} ~ p^r q^{k-r} \right ) \\ = \ln{(k-1)!} ~- \ln(k-r)! ~-\ln(r-1)! ~+ r\ln p + (k-r)\ln q $$
幾何分布は畳み込むことで負の二項分布になりましたね。
もちろんのことながら、負の二項分布を連続化した分布も考えることができます。
さらに言えば、指数分布を畳み込むことで同じ分布が得られるはずです。
それこそがガンマ分布(厳密に言えばアーラン分布)なわけです。
そこで、ここではガンマ分布を2つのやり方
① 負の二項分布の連続化
② 指数分布の畳み込み
で導出してみます。
① 負の二項分布の連続化
負の二項分布は、$$Pr(X=k) = ~{}_{k-1} \mathrm{C}_{r-1} ~ p^r q^{k-r}$$
と表わせ、「事象が試行k回目にちょうどr回生じる確率」の意味付けができます。
これを連続化すれば、おそらく
「事象が時間tのときにちょうどr回生じる確率分布」が得られるはずです。
まず、組み合わせの変形はそのままではやりづらいので、負の二項分布の自然対数を変形していくことにします。
また、非常に大きい数 x について、スターリンの近似式、
$$ \ln x! \approx x \ln x - x$$
が成り立つこと、そして、小さい数 x について、次の近似式が成り立ちます:
$$ \ln (1-x) \approx -x $$
$$\ln Pr(X=k) = \ln \left( ~{}_{k-1} \mathrm{C}_{r-1} ~ p^r q^{k-r} \right) = \ln \left( \frac{(k-1)!}{(k-r)! (r-1)!} ~ p^r q^{k-r} \right ) \\ = \ln{(k-1)!} ~- \ln(k-r)! ~-\ln(r-1)! ~+ r\ln p + (k-r)\ln q $$
スターリンの式で、$\ln(k-1)!$と$\ln(k-r)!$を近似し、$p=\phi dt$を代入すると
$$= (k-1)\ln(k-1)-(k-1) - (k-r)\ln(k-r) +(k-r) -\ln(r-1)!+r \ln(\phi dt)+(k-r)\ln(1-p)$$
ここで、次の近似、
$$\ln(k-a)=\ln k + \ln(1-a/k) \approx \ln k - \frac{a}{k} \\\ln(1-p) \approx -p = -\phi dt$$
を使うと、
$$= (k-1)\left(\ln k-\frac{1}{k}\right) - (k-r)\left(\ln k -\frac{r}{k}\right) +1-r -\ln(r-1)!+r \ln(\phi dt)-(k-r)\phi dt\\= (r-1)\ln k -\frac{1}{k} ((k-1)-r(k-r)) + 1-r -\ln(r-1)!+ r\ln\phi +r\ln dt -\phi t+r\phi dt$$
少し式が煩雑になってきたので、
$L = -\ln(r-1)!+r\ln\phi-\phi t$と置いて、式を整理していくと、
$$=(r-1)\ln k -\frac{1}{k} ((k-1)-r(k-r)) + 1-r +r\ln dt+r\phi dt + L\\=(r-1)(\ln t - \ln dt)-\frac{1+r^2}{k}+r\ln dt + r\phi dt +L\\=(r-1)\ln t + \ln dt - \left(\frac{(1+r)^2}{t} +r\phi \right )dt + L$$
ここで、Lというのは、
$$L = \ln \left( \frac{\phi^r \exp(-\phi t)}{(r-1)!} \right )$$
と変形できるので、これを使って変形すると、
$$= \ln \left( \frac{t^{r-1} \phi^r \exp(-\phi t)dt}{(r-1)!} \right) - \left(\frac{(1+r)^2}{t} +r\phi \right )dt\\ \approx \ln \left( \frac{t^{r-1} \phi^r \exp(-\phi t)dt}{(r-1)!} \right) ~~(\because dt \ll 1)$$
よって、
$$Pr(T=t) = \frac{t^{r-1} \phi^r \exp(-\phi t)}{(r-1)!} dt$$
となり、$Pr(T=t) = \Gamma (t) dt $とすれば、確率密度 Γ(t) は、
$$ \Gamma (t) = \frac{t^{r-1} \phi^r \exp(-\phi t)}{(r-1)!} $$
となります。
$$\ln(k-a)=\ln k + \ln(1-a/k) \approx \ln k - \frac{a}{k} \\\ln(1-p) \approx -p = -\phi dt$$
を使うと、
$$= (k-1)\left(\ln k-\frac{1}{k}\right) - (k-r)\left(\ln k -\frac{r}{k}\right) +1-r -\ln(r-1)!+r \ln(\phi dt)-(k-r)\phi dt\\= (r-1)\ln k -\frac{1}{k} ((k-1)-r(k-r)) + 1-r -\ln(r-1)!+ r\ln\phi +r\ln dt -\phi t+r\phi dt$$
少し式が煩雑になってきたので、
$L = -\ln(r-1)!+r\ln\phi-\phi t$と置いて、式を整理していくと、
$$=(r-1)\ln k -\frac{1}{k} ((k-1)-r(k-r)) + 1-r +r\ln dt+r\phi dt + L\\=(r-1)(\ln t - \ln dt)-\frac{1+r^2}{k}+r\ln dt + r\phi dt +L\\=(r-1)\ln t + \ln dt - \left(\frac{(1+r)^2}{t} +r\phi \right )dt + L$$
ここで、Lというのは、
$$L = \ln \left( \frac{\phi^r \exp(-\phi t)}{(r-1)!} \right )$$
と変形できるので、これを使って変形すると、
$$= \ln \left( \frac{t^{r-1} \phi^r \exp(-\phi t)dt}{(r-1)!} \right) - \left(\frac{(1+r)^2}{t} +r\phi \right )dt\\ \approx \ln \left( \frac{t^{r-1} \phi^r \exp(-\phi t)dt}{(r-1)!} \right) ~~(\because dt \ll 1)$$
よって、
$$Pr(T=t) = \frac{t^{r-1} \phi^r \exp(-\phi t)}{(r-1)!} dt$$
となり、$Pr(T=t) = \Gamma (t) dt $とすれば、確率密度 Γ(t) は、
$$ \Gamma (t) = \frac{t^{r-1} \phi^r \exp(-\phi t)}{(r-1)!} $$
となります。
② 指数分布の畳み込み
t秒後にちょうどk回起こる確率分布を$g_k(t)$とすると、k=2のときは2つの指数分布をたたみ込めばいいので、
$$g_2(t)=\int_0^t \left(\phi \exp(-\phi (t-t')) \right )\left(\phi \exp(-\phi t') \right )dt'\\ = \phi^2 \exp(-\phi t) \int_0^t ~dt' = t \phi^2 \exp(-\phi t)$$
となります。一応$g_3(t)$も求めてみると、これは$g_2(t)$と指数分布の畳み込みで求められ、
$$ g_3(t) = \int_0^t g_2(t') \phi \exp(-\phi(t-t')) dt' \\ = \int_0^t t' \phi^3 \exp(-\phi t) dt' = \frac{t^2 \phi^3 \exp(-\phi t)}{2!} $$
となります。
ここから帰納的に、
$$ g_k(t) = \frac{t^{k-1} \phi^k \exp(-\phi t)}{(k-1)!} $$
と仮定してみると、
$$g_{k+1}(t) = \int_0^t g_k(t') \phi \exp(-\phi(t-t'))dt' \\ = \int_0^t \frac{t'^{k-1} \phi^k \exp(-\phi t')}{(k-1)!} \cdot \phi \exp(-\phi(t-t')) dt' \\ = \frac{\phi^{k+1} \exp(-\phi t)}{(k-1)!} \int_0^t t'^{k-1} dt' = \frac{\phi^{k+1} \exp(-\phi t)}{(k-1)!} \cdot \frac{t^k}{k}\\ = \frac{t^k \phi^{k+1} \exp(-\phi t)}{k!} $$
ということで、やはりどちらの側からもガンマ分布が求められました。
ちなみに今回出した分布のパラメータ r は正の整数値をとりますが、実際のガンマ分布のパラメータ r は正の実数値を取ります。
ちなみに今回出した分布のパラメータ r は正の整数値をとりますが、実際のガンマ分布のパラメータ r は正の実数値を取ります。
そこで、正の整数値をとる場合の確率分布はアーラン分布と呼ばれています。ですから、これら一連の導出は厳密にはアーラン分布の導出ということになります。
さて、ガンマ分布の平均値と分散を求めてみましょう。愚直に計算してもいいのですが、どうせなら、負の二項分布を連続化、もしくは指数分布を畳み込んだものがガンマ分布ということを利用してみましょう。
負の二項分布の平均値と分散はそれぞれ、$\mu = r/p,~~ \sigma^2 = rq/p^2$となります。
ここに、変数変換 $T = X dt$を考慮しながら、 $p = \phi dt$ を代入すれば、
$$ E(T) = E(X dt) = E(X) dt = \frac{r dt}{p} = \frac{r}{\phi} \\ Var(T) = Var(X dt) = Var(X) dt^2 = \frac{r q dt^2}{p^2} = \frac{r}{\phi^2} $$
と求められます。
また、ガンマ分布に従う確率変数 Z と r個の指数分布に従う変数 $X_i$ は、
$ Z = X_1 + X_2 + ... + X_r$
であり、かつ、$X_i$ はそれぞれ独立なので、
$E(Z) = E(X_1 + X_2 + ... + X_r) = E(X_1) + E(X_2)+ ... + E(X_r) = r/\phi$
分散も同様に、
$Var(Z) = Var(X_1 + X_2 + ... + X_r) = Var(X_1) + Var(X_2)+ ... + Var(X_r) = r/\phi^2$
と求められます。
定義通りに求めるやり方は、練習問題としておきます。
さて、ガンマ分布の平均値と分散を求めてみましょう。愚直に計算してもいいのですが、どうせなら、負の二項分布を連続化、もしくは指数分布を畳み込んだものがガンマ分布ということを利用してみましょう。
負の二項分布の平均値と分散はそれぞれ、$\mu = r/p,~~ \sigma^2 = rq/p^2$となります。
ここに、変数変換 $T = X dt$を考慮しながら、 $p = \phi dt$ を代入すれば、
$$ E(T) = E(X dt) = E(X) dt = \frac{r dt}{p} = \frac{r}{\phi} \\ Var(T) = Var(X dt) = Var(X) dt^2 = \frac{r q dt^2}{p^2} = \frac{r}{\phi^2} $$
と求められます。
また、ガンマ分布に従う確率変数 Z と r個の指数分布に従う変数 $X_i$ は、
$ Z = X_1 + X_2 + ... + X_r$
であり、かつ、$X_i$ はそれぞれ独立なので、
$E(Z) = E(X_1 + X_2 + ... + X_r) = E(X_1) + E(X_2)+ ... + E(X_r) = r/\phi$
分散も同様に、
$Var(Z) = Var(X_1 + X_2 + ... + X_r) = Var(X_1) + Var(X_2)+ ... + Var(X_r) = r/\phi^2$
と求められます。
定義通りに求めるやり方は、練習問題としておきます。
登録:
投稿 (Atom)